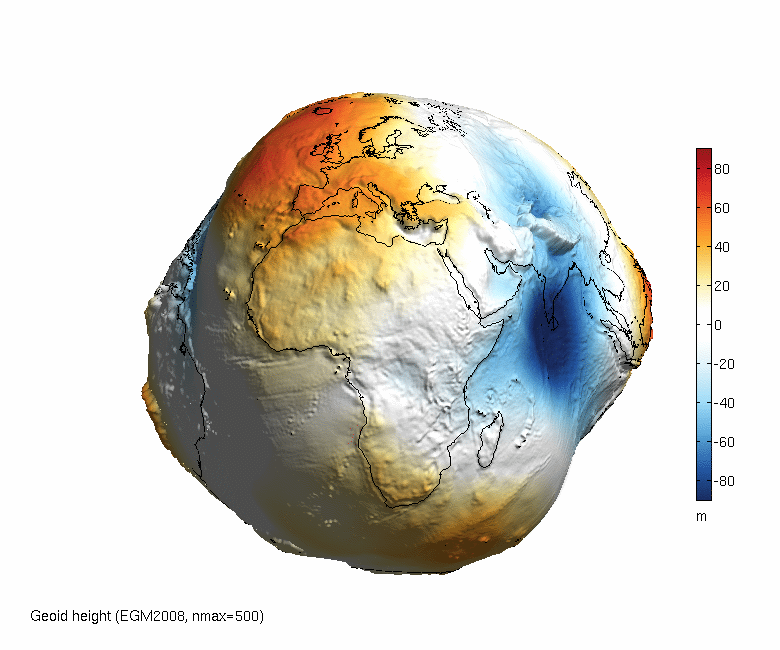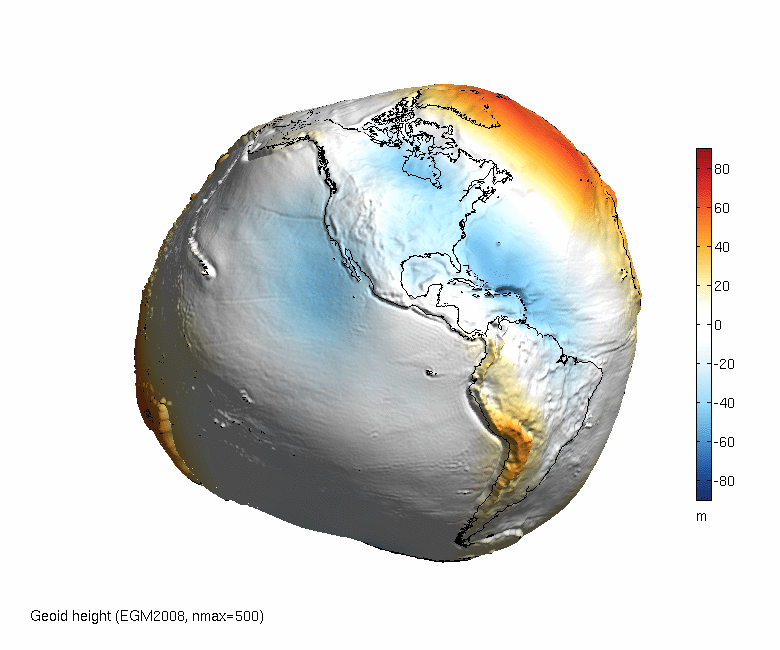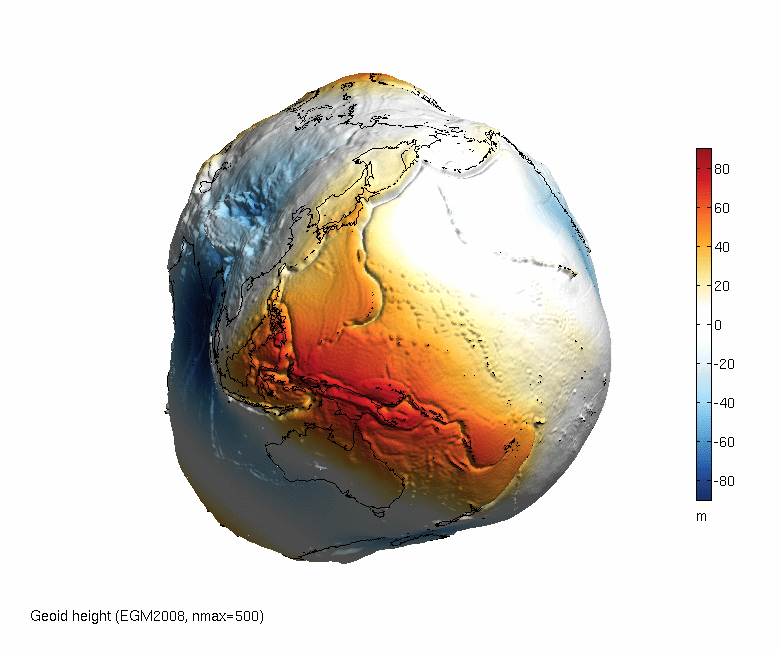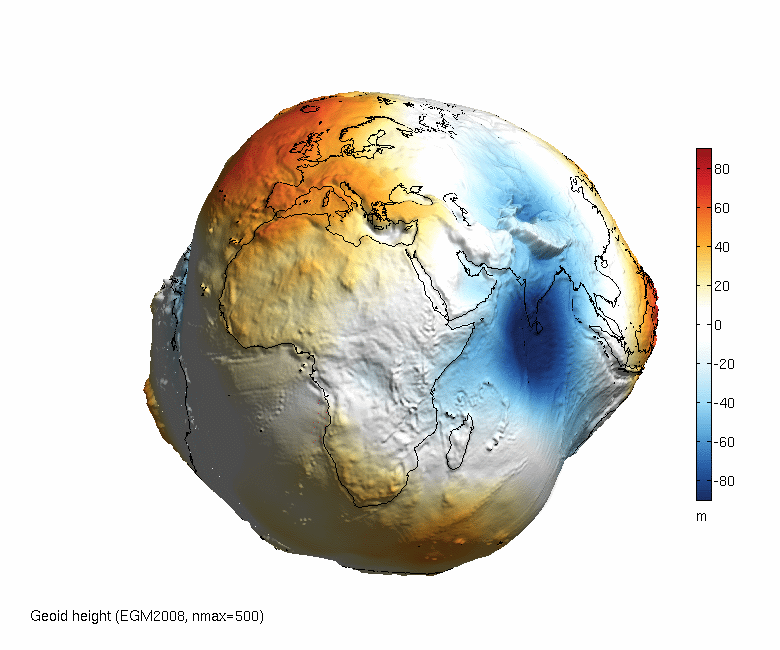
La forma real de la Tierra es un geoide siendo esta una superficie irregular debido a que la densidad de la Tierra no es constante en todos sus puntos, dicha irregularidad es la consecuencia de las anomalías gravimétricas que dichas variaciones de densidad ocasionan.
Conocer con exactitud el geoide es complicado; por lo tanto el intento más básico de establecer un modelo de la forma de la Tierra, es asemejándola a una figura geométrica simple, la cual pueda expresarse mediante una ecuación matemática. Además de ser más sencilla de manejar, disponer de esta ecuación matemática permite la aplicación de conceptos geométricos, estableciendo así una base práctica para el trabajo con coordenadas y la definición de sistemas de referencia.
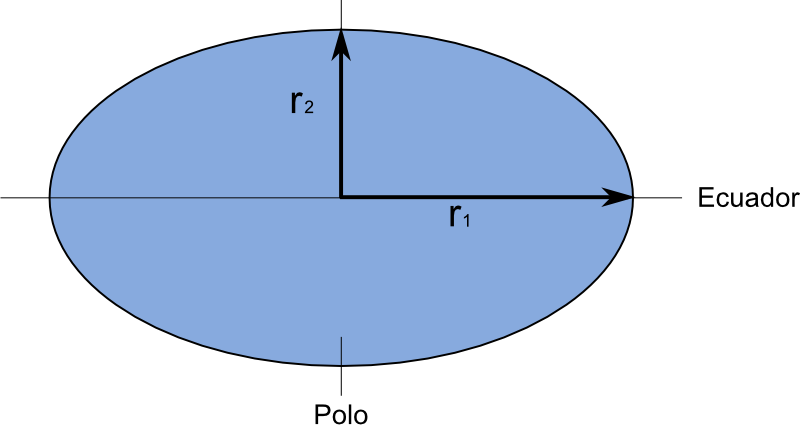
Como se muestra en la figura de abajo, un elipsoide viene definido por dos parámetros: el semieje mayor y el semieje menor. En el caso de la Tierra estos se corresponderían con el radio ecuatorial y el radio polar respectivamente. La relación existente entre estas dos medidas define el grado de achatamiento del elipsoide.
En particular, se establece un factor de achatamiento según
![]()
siendo r1 el semieje mayor y r2 el semieje menor.
Existen diferentes modelos de elipsoides utilizados en geodesia, denominados elipsoides de referencia. Las diferencias entre ´estos vienen dadas por los valores asignados a sus parámetros más importantes.
Debido a la evolución histórica de la idea de elipsoide de referencia, las medidas de los semiejes que lo definen no son únicas. Es decir, no en todos lugares y en todas las circunstancias se emplea un mismo elipsoide caracterizado por unos valores r1 y r2 idénticos. Esto es debido principalmente al hecho de que un determinado elipsoide no se adapta de modo igualmente preciso a todas las regiones terrestres, y el elipsoide que proporciona un mejor ajuste para un área dada (por ejemplo, un continente o país) puede no ser el mejor en otra zona de la Tierra alejada de la primera.
La siguiente tabla muestra algunos de los elipsoides de uso más extendido en diversas partes del mundo, con sus correspondientes parámetros.
Tabla 1: Modelos de elipsoides
| Elipsoide | Semieje mayor | Semieje menor | 1/f |
|---|---|---|---|
| Australian National | 6378160.000 | 6356774.719 | 298.250000 |
| Bessel 1841 | 6377397.155 | 6356078.963 | 299.152813 |
| Clarke 1866 | 6378206.400 | 6356583.800 | 294.978698 |
| Clarke 1880 | 6378249.145 | 6356514.870 | 293.465000 |
| Everest 1956 | 6377301.243 | 6356100.228 | 300.801700 |
| Fischer 1968 | 6378150.000 | 6356768.337 | 298.300000 |
| GRS 1980 | 6378137.000 | 6356752.314 | 298.257222 |
| International 1924 (Hayford) | 6378388.000 | 6356911.946 | 297.000000 |
| SGS 85 | 6378136.000 | 6356751.302 | 298.257000 |
| South American 1969 | 6378160.000 | 6356774.719 | 298.250000 |
| WGS 72 | 6378135.000 | 6356750.520 | 298.260000 |
| WGS 84 | 6378137.000 | 6356752.314 | 298.257224 |
Fuente: Libro SIG (V. Olaya)
Uno de los elipsoides de referencia más utilizados actualmente es el descrito en el sistema denominado World Geodetic System 84 (WGS-84), desarrollado por el Departamento de Defensa de los EEUU, y que tiene como origen el centro de masas de la Tierra. Su popularidad se debe a que es el utilizado por el sistema de posicionamiento global por satélite Global Positioning System (GPS).