Existen diferentes estructuras de datos vectoriales. Cada una de ellas tiene diferentes ventajas e inconvenientes; nosotros aquí examinaremos dos de los más comunes.
- El modelo de datos espagueti o Lista de coordenadas. Es la estructura de datos vectoriales más simple, en ella cada punto, la línea y/o polígono se representa como una serie de pares de coordenadas X, Y (o como un único par de coordenadas X, Y en el caso de un imagen vector de un solo punto) sin estructura inherente. Uno puede imaginarse cada línea en este modelo es una sola hebra de espagueti que se forma en complejas figuras mediante la adición de más y más hebras de espaguetis. Es notable que, en este modelo, los polígonos que se encuentran adyacentes entre sí, se deben hacer de sus propias líneas, o los soportes de espaguetis. En otras palabras, cada polígono se debe definir de forma única por su propio conjunto par de coordenadas X, Y , incluso si los polígonos adyacentes comparten exactamente la misma información del borde o límite. Esto crea algunas redundancias dentro del modelo de datos y por lo tanto reduce la eficiencia.
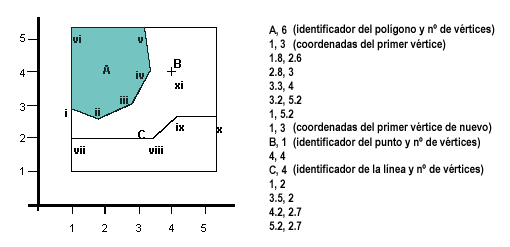
En resumen, este modelo es sencillo, fácil de operar, no almacena topología, presenta el inconveniente de registrar operaciones redundantes lo cual implica espacios de almacenamiento mayores y es muy utilizada en cartografía automática, esto último debido a que permite la reproducción eficiente de mapas y gráficos ya que esta información topológica es innecesaria para el trazado y la impresión.
- El modelo de datos topológico. Se caracteriza por la inclusión de información topológica dentro del conjunto de datos. La topología es un conjunto de reglas que modelan las relaciones entre puntos, líneas y polígonos vecinos, determinando la forma en que comparten geometría. Por ejemplo, considere dos polígonos adyacentes. En el modelo de espagueti, el límite común de dos polígonos vecinos se define como dos líneas separadas, idénticas. La inclusión de topología en el modelo de datos permite una sola línea para representar a este límite compartido con una referencia explícita, para indicar qué lado de la línea es la que pertenece al polígono. Topología también se ocupa de la preservación de las propiedades espaciales cuando las formas se flexionan, se extiende, o se colocan bajo transformaciones geométricas similares, lo que permite la proyección y reproyección de archivos de mapas más eficiente.
Disponer de topología en una capa vectorial es de gran importancia a la hora de llevar a cabo ciertos tipos de análisis, así como otros tales como la edición de los propios datos geográficos.
En la figura de abajo se puede observar la diferencia existente entre editar una capa de polígonos con topología y una sin ella. En el primer caso, la información contenida en la capa antes de su edición nos informa no solo de la forma de cada polígono, sino también del hecho de que ciertos polígonos comparten bordes comunes y de que el conjunto de ellos cubre el espacio de forma completa (constituyen una teselación). Así, al modificar un punto en uno de los polígonos, todos aquellos polígonos adyacentes que comparten dicho punto modifican también su perímetro. Las capacidades de edición implementadas en el Sistema de Información Geográfica hacen uso de la información topológica a la hora de editar geometrías. En el segundo caso, sin embargo, esta información no existe, y no se pueden alterar los polígonos adyacentes, perdiéndose la teselación completa del espacio.
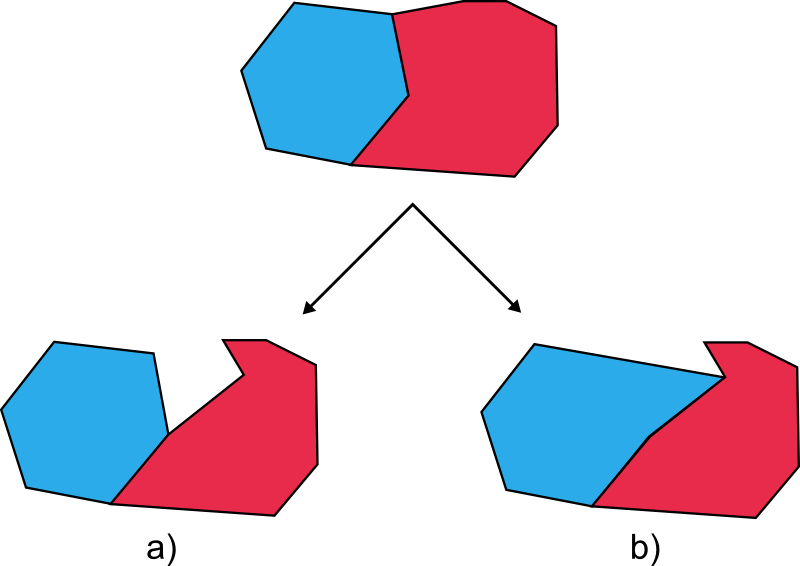
La topología es en este caso un elemento que contribuye a la calidad de los datos, pues mantiene la coherencia espacial de estos y evita la aparición de elementos tales como polígonos de muy pequeño tamaño, frecuentes en la digitalización de entidades debido a las pequeñas imprecisiones que se presentan en el proceso, y que causan la presencia de falsos solapes entre polígonos.
No obstante, no todos los SIG incorporan capacidades de manejo y análisis de capas vectoriales con topología, y son menos aún los que implementan capacidades para crear dicha topología. En general, estas han quedado reservadas a las aplicaciones de alta gama, y el manejo de información vectorial en los SIG de escritorio no incluye de forma general lo relativo a la topología.
-
Para conocer otros tipos de estructuras de datos vectoriales se recomienda revisar http://www.geogra.uah.es/gisweb/1modulosespanyol/IntroduccionSIG/GISModule/GIST_Vector.htm
-
Si desean profundizar sobre topología se recomienda revisar el tema Vector Data Models Structures desde http://2012books.lardbucket.org/books/geographic-information-system-basics/s08-data-models-for-gis.html